On the Problem of City Boundaries

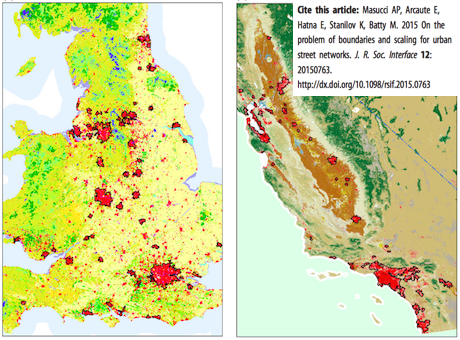
Paolo Masucci led this study based on defining city boundaries – one of the key research issues in CASA on our Mechanicity project – introducing a really simple idea that cities grow to a condensation threshold after which the city is ill-formed. The threshold can be detected using clustering and in some senses the giant cluster sets this boundary. We show here how UK cities and cities in California, when normalized, collapse onto the same logistic curve which defines the point at which this threshold and hence boundaries can be determined. Here is the abstract of the paper below. Click here to get the PDF but if you want to get the open access paper in the Journal click here instead.

“Urban morphology has presented significant intellectual challenges to mathematicians and physicists ever since the eighteenth century, when Euler first explored the famous Konigsberg bridges problem. Many important regularities and scaling laws have been observed in urban studies, including Zipf’s law and Gibrat’s law, rendering cities attractive systems for analysis within statistical physics. Nevertheless, a broad consensus on how cities and their boundaries are defined is still lacking. Applying an elementary clustering technique to the street intersection space, we show that growth curves for the maximum cluster size of the largest cities in the UK and in California collapse to a single curve, namely the logistic. Subsequently, by introducing the concept of the condensation threshold, we show that natural boundaries of cities can be well defined in a universal way. This allows us to study and discuss sys-tematically some of the regularities that are present in cities. We show that some scaling laws present consistent behaviour in space and time, thus suggesting the presence of common principles at the basis of the evolution of urban systems.”